:)

A Prova

         O filme é baseado na história de Catherine, uma jovem que viveu anos em virtude de seu pai que sofria de esclerose, após sua morte ela teme herdar os problemas mentais de seu pai, com isso, se isola de todos em sua casa, mas em pouco tempo, até que chega sua irmã querendo vender sua casa para morar com ela e um ex-aluno de seu pai interessado em pesquisas de seus cadernos para saber se tem alguma lógica um grande matemático com mais de 100 cadernos escritos sobre a matemática ter esclerose. Ele queria entender como era possível tamanha genialidade com tamanha insanidade.

Quino, desiludido com o século

Quino, o cartunista argentino autor de Mafalda, desiludido com o rumo deste século no que diz respeito a valores e educação, deixou impresso no cartoon o seu sentimento:

A genialidade do artista faz uma das melhores críticas sobre a criação de filhos (e educação) nos tempos atuais.

 

Muito legal!

 

Vamos fazer uma festa?

Público Alvo
Crianças de 10 anos. 5° Ano do Ensino Fundamental.

Justificativa

Em comemoração ao dia das crianças e dia do professor uma comemoração deveria ser feita. Os alunos gostaram da ideia e partindo do interesse em organizar a festa, alguns cálculos deveriam ser feitos.

Objetivo

Trabalhar questões matemáticas relacionadas ao uso das operações na nossa vida diária;

Trabalhar multiplicação e divisão como parte do cálculo essencial e facilitador;

Identificar mililitros e litro;

Relacionar e transformar litro em ml;

Estimular o trabalho em equipe;

Refletir sobre o consumo excessivo e sobre questões relacionadas ao uso do dinheiro;

Estratégia

Dispondo a sala em círculo propus questões norteadoras que moveram o trabalho e incitaram respostas:

Quantos alunos temos na sala?

Quantos salgadinhos comemos quando vamos a uma festa?

E refrigerante, quantos litros tem numa garrafa?

Quantos copos de refrigerante cada um consomem quando está numa festa?

Quantos ml tem a caneca plástica em que bebemos o refrigerante?

Quantos brigadeiros comemos quando vamos a uma festa?

Quanto dinheiro será gasto em cada um desses elementos?

Qual será o total de dinheiro que empreenderemos em nossa festa?

Quanto ficará para cada um?

Metodologia

A partir das questões norteadoras, as respostas foram dadas até que chegamos ao resultado final. Todos deveriam anotar os resultados obtidos no seu caderno de matemática.  Os alunos foram convidados a fazer os cálculos na lousa também (uma vez cada um). Temos 18 alunos na sala. Cada um respondeu quantos salgadinhos comia e tiramos uma média. Começamos do número 5.

4 responderam 5;

1 respondeu 6;

8 responderam 8;

5 responderam 10.

O maior número de pessoas (8) responderam 8 e o segundo lugar ficou para os que responderam 10.  Fizemos a média entre 8+10 = 18:2 = 9. Então, 9 seria a quantidade que encomendaríamos por pessoa.

Mas quantos alunos temos? 17 e a uma professora = 18 pessoas.

Vamos multiplicar o número de salgados por pessoa para ver quantos salgados serão necessários: 9x18 = 162.

E brigadeiro quanto comemos? Começamos do 3.

5 responderam 3;

6 responderam 4;

5 responderam 5;

2 responderam 6.

Em primeiro lugar ficou 4 e em segundo 3. Contudo, como a média dava fracionada optamos por 4.

4x18 = 72  docinhos.

Quantos copos de refrigerante bebemos?

11 responderam 3;

4 responderam 4;

2 responderam 2;

1 respondeu 1.

Votamos pela maioria e ficamos com a média de 3 copos.

Quanto cabe de refrigerante dentro das nossas canecas de água. Quantos litros tem uma garrafa de refrigerante?

No copo medidor vimos que nas nossas canecas cabem 180 ml.

O refrigerante mede 2l?

1 litro corresponde a 1000 ml.

2000 ml de refrigerante por garrafa.

Cada um consumirá 3 copos 3x180 = 540 ml por aluno.

540 x o número de alunos  (18) = 9720 litros de refrigerante.

Se cada garrafa tem 2 litros de quantas precisamos para que tenhamos 9.720 litros.

5 garrafas tem 10 litros e sobram 280 ml.

E o bolinho? Quantos precisamos? Qual sabor? Todos votaram chocolate. Precisamos de 18.

Custo total:

Quanto dinheiro precisaremos?

Salgado = a unidade sai por R$ 0,40.

0,40x162 (número de salgados que julgamos necessário) = 64,80.

Bolinho/ Cup cake.

A unidade custa R$ 3,00.

3x18 (número de pessoas da festa) = 54,00.

A unidade do docinho custa também R$ 0,40.

0,40x72 (número de docinhos que julgamos necessário) =28,80

A unidade do refrigerante custa R$ 4,50.

4,50x5 (número de garrafas necessárias) = 22,50.

64,80+54+28,80+22,50 = 170,10.

O total a ser gasto é de R$ 170,10.

Mas quanto será gasto por pessoa? Como podemos calcular?

170:18 (número de pessoas) =  R$ 9,40 por pessoa.

Avaliação

A avaliação foi feita durante o processo com a participação e questionamento dos alunos e todo conhecimento prévio foi considerado. Quanto ao novo conceito aprendido sobre litro e mililitro outras atividades serão propostas durante a semana para reforçar as relações.

Resultado

A atividade proposta chamou atenção das crianças que se mantiveram interessadas e surpresas com a importância das relações matemáticas no nosso cotidiano. Ao mesmo passo que alguns começaram a refletir sobre questões relacionadas ao dinheiro e ao consumo excessivo.

Situações em que são utilizadas as operações matemáticas

1. Quando tenho que medir a quantidade de colheres de achocolatado que quero colocar no meu leite.

2. Quando olho no relógio para saber a hora e calcular quanto tempo falta para o intervalo.

3. Quando coloco algo para descongelar no microondas e tento calcular o tempo pela quantidade de gelo que o alimento tem.

4. Quando preparo uma receita que está em gramas, litros, ml, mg e transformo a informação em colheres, copos, etc.

5. Quando calculo o trajeto que o ônibus fará até a minha casa.

6. Quando calculo quanto receberei de troco de algo que comprei.

7. Quando vou ao caixa eletrônico depositar ou sacar dinheiro.

8. Quando vou à feira e os alimentos são pesados e a partir do peso é determinado o valor que vou pagar.

9. Quando utilizo os créditos do celular e vejo quantos minutos usei, quanto será descontado e quantos reais ficarão em crédito.

10. Quando coloco o condicionador de cabelo na mão antes de colocar na cabeça para ver se está aquém ou além da quantidade necessária.

11. Quando olho o galão de água e vejo quanto ainda falta para acabar e calculo mais ou menos o consumo diário para me certificar em quantos dias vai acabar e terei que trocá-lo.

12. Quando coloco uma calça apertada e penso quantos kgs terei que ter a menos para a calça se ajustar ao corpo.

13. Quando encho o balde para lavar a cozinha e vejo quantos baldes de água são necessários para tirar o sabão espalhado no chão que esfreguei.

14. Quando estou lendo um livro e calculo quantas páginas faltam para acabar o capítulo, quantos parágrafos faltam para acabar a página e quantas linhas faltam para acabar o parágrafo.

15. Quando faço a chamada e na roda conto a quantidade de alunos.

16. Quando multiplico quantos litros de gasolina por km vou utilizar, quantos km vou percorrer por semana e quanto de gasolina terei que colocar no carro.

17. Quando estou atrasada de manhã e tento reduzir meu tempo para cumprir as tarefas essenciais.

18. Quando tento dividir igualmente as peças do brinquedo de encaixar entre as crianças.

19. Quando como um chocolate e calculo quantas calorias tem o alimento e quantas teria que gastar para não engordar.

20. Quando calculo quantos salgados são necessários por pessoa e quanto sairá cada salgado.

21. Quando calculo a quantidade de bebida necessária por pessoa e quantos litros de bebida serão necessários.

Exemplos de atividades feitas com ábaco

1 - Com o seu ábaco vamos representar o número 530. Quantas peças teremos na centena, na dezena e na unidade?

Resposta:  5 peças na centena;

                 3 peças na dezena;

                 0 na unidade.

 

2 - O número representado no ábaco é ________.

    

 

 

 

 

 

 

 

 

 

 

Resposta: 265.

3 - Descubra o resultado. Qual é o número representado na parte debaixo do ábaco? Qual é o número representado na parte de cima?

Resposta:  Número representado embaixo 167;

                Número representa em cima 265.

4 - Qual é o resultado dessa adição?

 

 

A) Primeiro junte no seu ábaco dez unidades e troque por uma dezena.

 B)    Depois junte um grupo de dez dezenas e troque por uma centena.

Resultado: 432.

O homem que calculava

É isso

Atividade de Divisão

Leia a história com atenção e ajude as formigas a solucionarem o problema.

Era uma vez...

Três (3) formigas amigas: Formigordinha, Formimagrinha e Formosura. Todos os dias, com a ordem da rainha, elas saíam bem cedinho do formigueiro para recolher alimentos. Trabalhavam como coletoras.

Elas entregavam tudo que recolhiam para a formiga contadora, que se chamava Formicontinha. Formicontinha anotava e calculava tudo, principalmente quantas folhinhas cada formiga trazia.

 

Numa tarde, enquanto as três formigas coletoras estavam levando os alimentos para Formicontinha contar, um grande estrondo se ouviu no formigueiro. Era alguém apaixonado que, distraído, quase tropeçou no formigueiro. Após o susto, um grande problema apareceu: todas as folhas que as três coletoras recolheram estavam caídas no chão e Formicontinha ainda não tinha anotado e calculado.

 

As formigas sabiam que no total tinham 15 folhas caídas e que naquele dia elas haviam recolhido a mesma quantidade de folhas.

 

 

E agora, quantas folhas cada uma das formigas havia recolhido? Formicontinha já estava maluca de tanto contar. Vamos ajudá-las a desvendar o mistério dessa divisão?

Cole nos círculos as folhinhas para saber quantas cada formiga recolheu.

 

Resposta: Cada formiga recolheu _______folhas.

 

 

 

 

 

 

 

A equação do amor

    A matemática é uma ciência que muitos odeiam, sentem pavor só de ouvir seu nome, terminam suas vidas com um sentimento de desprezo por equações, expressões, sentenças e problemas. Por outro lado, há pessoas que a admiram, têm verdadeira adoração pelos seus mistérios, teoremas e axiomas, conseguem ver em suas entrelinhas inspiração para relatos de amor e paixão. Galileu Galilei descreve sua admiração pela matemática com o célebre pensamento: "A matemática é o alfabeto com o qual Deus escreveu o universo". Seguindo a linha dos que têm muito apreço por essa ciência fascinante, vamos exibir uma equação que poderá servir para conquistar alguns corações, mesmo daqueles que ainda não sentiram brotar no peito a paixão pela matemática. Reparem na beleza da estruturação e mais ainda no resultado final, uma verdadeira declaração de amor.

Vamos considerar os números reais positivos a, t, e, o, m. Obteremos o valor real de x na equação:

 

Vamos elevar os dois membros da igualdade ao quadrado, obtendo:

Multiplicando ambos os membros por mo (sendo mo ≠ 0), obtemos:

Considerando a ≠ 0, vamos dividir os dois lados da igualdade por a, obtendo:

Por Marcelo Rigonatto
Matemático - Equipe Escola Kids

http://www.escolakids.com/a-equacao-do-amor.htm

Atividades

 

 

 

 

 

 

 

 

 

 

  

 

 

 

  

 

 

 

 

http://amoaeducacaoinfantil.blogspot.com.br/2009/03/atividades-de-matematica.html

Que lição tirar de Gênio Indomável?

Por maior que seja o conhecimento sobre determinada área, é preciso obter formação humana para viver plenamente.
 

 

 

 

 

 

 

 

 

Genialidade lógica não equivale a inteligência emocional.

 

Filme: Gênio Indomável, dirigido por Gus Van Sant, com Matt Damon e Robin Williams, 1997.
A história: Will Hunting (Matt Damon) tem 20 anos e já registrou algumas passagens pela polícia. Trabalhando como servente em uma universidade, se revela um gênio em matemática. Ele faz terapia, por decisão judicial, mas não apresenta resultados de melhora porque debocha de todos os analistas. Até encontrar um com quem de se identifica.
Quem indica: O jornalista e escritor Eduardo Torelli. "A obra destaca a diferença entre inteligência e conhecimento, bem como a relevância do meio social na formação de um indivíduo. No entanto, o maior "aprendizado" do protagonista se dá por meio de um psicólogo que trará à luz os traumas e recalques do jovem super-dotado, para transformá-lo em um adulto capaz de exercer plenamente as potencialidades."
Por que ver: "Conhecimento não é tudo. O protagonista é muito bom matemática, mas em termos emocionais é uma criança de cinco anos. É muito legal perceber como a genialidade não é sinônimo de sucesso. Também é interessante mostrar o intelecto como uma forma de dar valor à sua vida, ao bem-estar. Ele é o típico aluno que pode decorar Shakespeare, mas nunca o sentiu", diz Leandro Alcerito, professor de biologia do Colégio Vértice, de São Paulo.
Que bom exemplo tirar: "Perceber como o saber construído pode servir de metáfora. As soluções dos problemas matemáticos são apresentados como soluções para problemas da vida, o que às vezes pode ser aplicado em sala de aula", observa o professor de artes, filosofia e sociologia Zilton Salgado.

 

 

Por

Gabriel Navarro
 

http://educarparacrescer.abril.com.br/aprendizagem/genio-indomavel-412767.shtml

:)

Somar é legal

Ábacos

O ábaco de pinos ou ábaco vertical.

Este ábaco pode ser feito de madeira ou sucatas e equivale ao mesmo sistema que o ábaco horizontal. Contudo, possui uma vantagem quanto à movimentação das peças que podem ser retiradas. Cada pino condiz com uma posição no sistema de numeração decimal. O primeiro pino da esquerda para direita representa a unidade, o posterior a dezena e o imediatamente posterior à centena e assim sucessivamente. Neste modelo cada vez que se agrupam 10 peças em uma haste ela deve ser trocada por uma peça que deve ser colada no pino à esquerda.

O ábaco e a numeração decimal

Diariamente, ao nos depararmos com alguma situação em que seja necessário o uso da aritmética, utilizamos automaticamente o sistema decimal. Contudo, esta é uma grande questão para aqueles que iniciam as primeiras compreensões sobre o referido sistema.

Compreender o sistema decimal, também foi um grande progresso na história da humanidade. Quando o homem utilizou uma pedrinha como representação simbólica dos seus dez dedos. Portanto, a representação do número 10 iniciou-se aquilo que poderia ser as primeiras premissas sobre o ábaco há aproximadamente 5.500 anos atrás na Mesopotâmia.

O ábaco é o mais antigo instrumento de cálculo e possui a mesma lógica que o nosso sistema de numeração, podemos dizer que é a representação concreta do sistema decimal. Nele é determinante o valor posicional, pois dependendo da posição em que se os números se encontram valores diferentes serão assumidos.

Utilizar esse recurso auxilia a criança na compreensão das regras do sistema de numeração decimal, além de ajudá-la nos procedimentos de cálculo e no desenvolvimento da memória.

Há vários tipos de ábaco, porém todos obedecem aos mesmos princípios e são variações do ábaco horizontal e do ábaco vertical.

O ábaco horizontal é constituído de uma moldura de madeira ou plástico onde estão afixados fios que podem ser de arame, madeira plástica ou linha. Esses fios formam linhas paralelas e podem ser denominados de fileiras. Em cada fileira correm dez contas. A primeira fileira representa a unidade, a segunda a dezena, a terceira a centena, a quarta a unidade de milhar, a quinta a dezena de milhar, a sexta a centena de milhar, a sétima a unidade de milhão, a oitava a dezena de milhão, a nona a centena de milhão.

Festa para comemorar ou festa para calcular?

Aproveite a oportunidade da festa do dia das crianças e calcule junto com seus alunos os gastos que serão necessários. Coloque-os como corresponsáveis pela organização do evento. Essa foi a proposta que fizemos com os alunos do 5° Ano do Ensino Fundamental na rede privada da cidade de Campinas/SP.

A partir de uma votação sobre o que comeríamos e quanto comeríamos, calculamos a despesa da festa e quanto seria a divisão por pessoa.

O resultado foi uma festa muito gostosa e uma lição muito importante de matemática.

Por
Ana Carolina Santos

Multiplicando com os dedos

Você sabia que pode utilizar os dedos para realizar multiplicações entre números de 6 a 10? Para isso, é necessário identificar os dedos da seguinte forma:
 

 

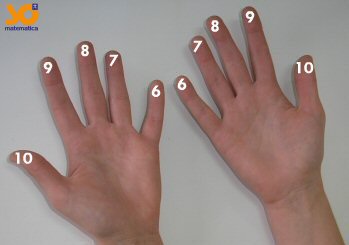
Por exemplo, para calcular 8x9, encosta-se o dedo equivalente ao 8 no dedo equivalente ao 9 na outra mão, como mostra a figura abaixo.
 

 

O resultado será um número de dois dígitos, onde o dígito das dezenas será igual à soma dos dedos que estiverem abaixo (incluindo os que estão em contato), e o dígito das unidades será igual à multiplicação dos dedos que estiverem acima. A figura a seguir ilustra a multiplicação.
 

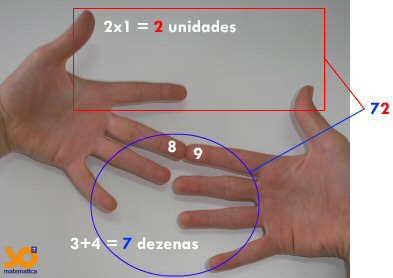
http://www.somatematica.com.br/curiosidades.php